Introduction
This page describes my explorations while writing a computer program to draw
cellular automata.
For those unfamiliar cellular automata, the idea is simple.
You can think of them as pictures that are created iteratively (e.g., row-by-row) using a set of simple rules, starting
from some initial data (e.g., a first row). For the type that I chose to create, we start with a grid whose boxes are blank,
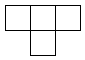
and color in one box in the first row. Then, move down one row. Each box in that row will then be either colored or not,
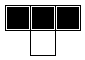
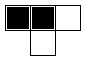
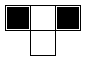
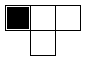
depending on a rule that incorporates the three boxes above it in the previous row (above to the left,
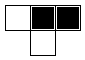
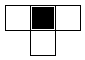
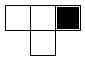
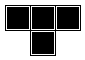
directly above, and above to the right). Here's part of the grid, illustrating the boxes on which
the bottom box depends.
|
Continue coloring boxes in this manner, going down one row at a time. For practical purposes,
it is easy to make the first colored box in the top row, middle column. Also, since the grid will
have finite width, we have to be careful with the boxes on the edges. I'll say more about that in a moment.
The Rules
How do we make the "rules" for creating an automaton? First, let's consider, as above, an individual
box, and the three boxes above it in the previous row. How many possible configurations are there for the
three boxes? Still assuming that a box can either be colored or blank, there are \(2^3 = 8\) configurations.
That is, two choices for the first box, times two choices for the second box, times two choices for the last
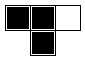
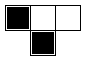
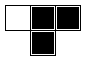
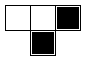
box. Here are the eight configurations.
To determine a rule, we must look at each configuration and then decide to either color the corresponding
lower box or leave it blank. This gives two choices per configuration, so there are \(2^{2^3} = 2^8 = 256\) rules.
For example, the images above determine a (boring) rule, but here is another.
Here is the beginning of the automaton determined by this rule.
Fixed Width, Arbitrary Height
Addressing the above unresolved question, what happens if we want the image to be of arbitary
height, while the width is constrained? My solution to this was to make the image "cylindrical"
in the following sense: the left-most box in a row sees the box right above it, the box to the
upper right, but since there no box to the upper left, it uses the right-most box in the previous
row. Similarly, the right-most box in a row sees the left-most box in the previous row. This way,
we can create an image as tall as we like, but with a fixed width. This was implemented using
modular arithmetic. If the image has width \(w\), then the boxes above the \(i\)-th box in a row
are \((i-1) \mod w\), \(i \mod w\), and \((1+1) \mod w\).
Colors, and More Examples
Aesthetically speaking, there is no good reason to only use black and white all the time, so
we might as well allow for any pair of colors to be used, one for "blank" and one for "colored".
Also, there the question of the first row. Why should it be blank except for one box? I thought
starting with random input on the first row might make for more interesting images. Also, I though
one might like the ability to increase the box size some magnification factor. These ideas went into the
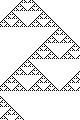
first version of the program (see below), which generated the following examples --click to enlarge.
A quick glance at a few of these images reveals a (perhaps) startling feature. Even though these
automata are all described by a small set of very simple rules, their behavior is emphatically not
simple! Chaos and randomness (unrelated to the randomness in the first row!) emerge seemingly from
nowhere in all but the most basic examples. Much has been studied regarding just how "random" things
can get. For example, they are random enough to be used as
pseudorandom number generators
in Mathematica.
Here's a bunch of links with way more information.
More Colors
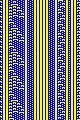
Another natural question to ask is, "What is so special about two colors?" The answer, of course,
is "nothing." The next modification to the program was to consider 3 colors, and then arbitrarily
many colors. As the number of colors increases, so does the complexity. This is apparent in the
number of possible rules. For the three boxes above a given box, we have \(3^3 = 27\) possible
configurations. If for each such configuration we must select a color from three, then there
are \(3^{3^3} = 3^27 = 7,625,597,484,987\) rules! That is roughly a thousand rules for each
person on earth! Here are some results.
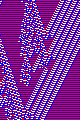
I pasted together some series of images generated by the same rule.
Even More Colors
To count the number of possible rules of an arbitrary number, say \(n\), of colors, we follow the
same procedure. There are \(n^3\) configurations, and each has \(n\) choices associated to create
a rule. This means there are \(n^{n^3}\) possible rules. This immediately ruled out a nice interface
for selecting a rule, so I opted to allow only random rule generation.
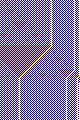
One thing I noticed was that the "interestingness" of the images peaks at around 3 or 4 colors. When
there are too many colors, things look too random, like colorful static. Here are some examples.
Other Types
There are further generalizations of the rules that were used up to this point. Why limit the effect
of the previously drawn rows to just the three boxes that are directly above the given box. The coloring
of a box could depend on any number of boxes from any number of previous rows. This makes things much,
much more complex. Namely, if we create a rule using \(k\) total boxes and \(n\) colors, then there are
\(n^{n^k}\) possible rules. For the \(n\)-color version, I gave a few choices for what boxes go into making
a rule. Here's a picture illustrating the new rules.
The Program
Here is the program, which runs inside a webpage (although you'll need a good web browser
for it to work properly).