What is a complex mapping?
A complex mapping is a function that takes a complex number as input and returns another complex
number as output: \(f: U \rightarrow \mathbb{C}\) for some domain \(U \subseteq \mathbb{C}\). Visualizing
such a function is a bit more complicated than visualizing a real-valued
function of a real variable, whose graph is simply a curve in the plane. The graph of a complex mapping
would be a surface in 4-dimensional space, which is not so easy to see! Therefore it makes more sense
to viualize a complex mapping another way, namely by observing how it acts on a region in the plane.
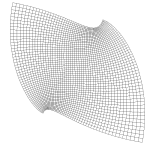
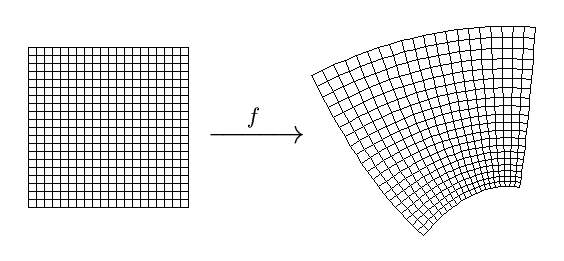
For example, the picture below illustrates how a complex mapping \(f\) deforms a square in
the plane. Complex mappings are the basic objects of study in
complex analysis.
The Program
Here is a program to visualize complex mappings. Note that it is not optimized for mobile web browsers.
The program can draw three types of mappings, described below.
Polynomials
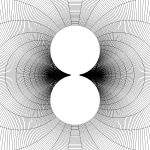
Complex polynomials are the
similar to regular polynomials over the real numbers, except the coefficients and
variables are now complex numbers. The generic form in the program is a degree 3, i.e., a cubic:
\[ A z^3 + B z^2 + C z + D \]
Here are a few examples of how complex polynomials behave.
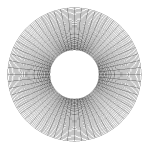
Mobius Transforms
A Mobius transformation
(also called fractional linear transformations) have real analogs, but they are not as
interesting. The complex versions, however, constitute a very important and interesting class
of functions. An amazing video describing their nature can be found
here.
\[ f(z) = \frac{A z + B}{C z + D}, \qquad AD - BC \ne 0. \]
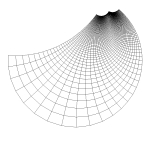
Here are a few examples of how Mobius transformtions behave.
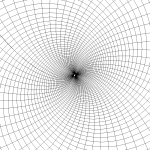
Exponentials
The exponential function
is perhaps the more important function in mathematics. The complex version combines the
"exponential growth" familiar from the real version with rotation in the plane. In fact,
it is periodic, something one might never guess from looking at the real version.
\[ f(z) = \exp(Az + B) + C \]
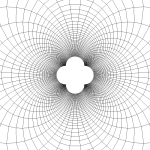
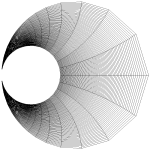
Here are a few examples of how complex exponentials behave.